硬间隔支持向量机要求训练数据是完全线性可分的,否则会宕机(无法工作);软间隔支持向量机则允许很少量的样本线性不可分,模型的容错能力相对前者好一点;但是,对于非线性问题应该如何处理呢,怎么用一个平面将二维平面中的两个不同半径的同心圆分隔开,怎么将高维线性不可分的图形分隔开,在实际应用中,遇到非线性问题(大部分都是),如何用SVM解决?这就需要引入核函数的概念了。
核函数定义
李航在《统计学习方法》中对核函数的定义如下:

核函数原理
先上总结:简单来说,核函数就是内积,或者说是用来计算映射到高维空间之后的内积的一种简便方法。
我们现在来细看下,核函数到底是个什么东西。在支持向量机(一) 中,我们已经推导出来,分类函数为:
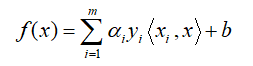 (1)
(1)其中,$x_i^Tx$其实就是向量内积,可以用$<·,·>$表示。
继续开篇提的问题,如下图,怎么用一条直线将二维平面中的两个不同半径的同心圆分隔开?

设上面的点用$x=(x_1,x_2)$ 表示,如果直接基于分类函数(1)找一个平面将两个圆分割开,这样肯定不行,因为在二维平面上无论怎么调整,你都无法找到一条直线完好地区分上图中的两个圆。
但是换个角度看可能就不一样了,我们把它映射到三维空间看一下。

通过将数据从二维平面映射到三维空间,两个无法线性分隔的图形变成线性可分的了。这里使用的映射函数是$\phi(x)=(x_1^2,\sqrt{2}x_1x_2,x_2^2)$。

再看下面这个例子,如何用一条直线将两类不同颜色的点分开,显然在二维平面上无论怎么划分都无济于事。

类似的方法,可以将这些点映射到三维空间,然后用一个平面将这两类数据轻易地区分出来。这里使用的映射函数是$x=(x1,x2,x1*x2)$

上面两个例子,套路都是:本来非线性的数据,找到一个映射函数,将其从低维映射到高维,然后在高维空间用线性分类方法将数据分割开来。
到目前为止,推理起来都比较顺畅,现在针对上面的例子做一些延伸,针对一个二次曲线,可以表示成:$$a1X_1 + a2X_1^2 + a3X_2 + a4X_2^2 + a5X_1X_2 + a6 = 0$$
构造一个五维空间,其中五个坐标的值为$$Z1 = X_1;Z2 = X_1^2 ;Z3 = X_2;Z4 = X_2^2 ;Z5 = X_1X_2$$
如果是一个三维曲线,那么需要构造一个19维的空间,可以看到,这个映射空间的维度会随着原空间维度的增加而成指数增长,这给会给$\phi(\cdot)$的计算带来了非常大的困难,而且如果遇到无穷维的情况,就根本无从计算了。更何况,映射到高维空间数据是否就线性可分还不一定呢。
如果我先在低维空间计算好两点之间的内积呢,这样就无需先映射到高维空间找映射函数,然后在根据映射函数计算内积了。针对第一个例子,设曲线上的任意两点为$x=(x_1,x_2),y=(y_1,y_2)$,其映射函数为$\phi(x)=(x_1^2,\sqrt{2}x_1x_2,x_2^2)$,那么映射函数计算内积后其实是跟$ x\cdot y $ 的平方的结果一样的,对应的核函数为。


这样的话,针对三次曲线方程或者更高维曲线方程,无需先映射到高维空间,可以直接将两点之间的内积代入分类函数求解未知参数。这种直接在低维空间中计算内积的方法就称为核函数或者核技巧。
核函数真正强大之处在于,只需要定义核函数 在低维空间进行内积计算,而不需要显式地定义映射函数,这对本来就是高维或者无限维的特征空间来说尤为有效。另外,映射函数并不是唯一的,比如还是回到第一个同心圆的例子,映射函数可以是$\phi(x)=(x_1^2,\sqrt{2}x_1x_2,x_2^2)$,也可以是$\phi(x)=(x_1,x_2,x_1^2+x_2^2)$
在低维空间进行内积计算,而不需要显式地定义映射函数,这对本来就是高维或者无限维的特征空间来说尤为有效。另外,映射函数并不是唯一的,比如还是回到第一个同心圆的例子,映射函数可以是$\phi(x)=(x_1^2,\sqrt{2}x_1x_2,x_2^2)$,也可以是$\phi(x)=(x_1,x_2,x_1^2+x_2^2)$
网上其实有很多关于SVM、核函数的讲解和讨论,关于讲解可以参考支持向量机通俗导论(理解SVM的三层境界)讲得是真心好。关于讨论可以参考知乎上的一个问题:机器学习有很多关于核函数的说法,核函数的定义和作用是什么?
核函数类型
sklearn 中,可选的核函数有以下四种:
- 线性 :

- 多项式:

- RBF :

- sigmoid:

后记
核函数的作用其实很简单,一言蔽之,就是计算映射到高维空间之后的内积的一种简便方法或者技巧,它能够将原本需要在高维空间计算的内积直接在原特征空间进行,无需变换空间。
说实话,写的这几篇文章中,核函数这篇是最耗时的,写到这里,感觉我对kenel trick 的理解还是很懵懂,不深刻,比如kenel 可以往那些方面进行推广、在实际应用中应该怎么选择kenel。写本文的时候,希望能够尽量通俗易懂地把它写明白,但是通俗易懂的前提是自己对这些概念的理解要很深入,所以在写的过程中出现过几次定好思路,写了大部分的时候发现不理想,重新整理的情况。不过从应用层面来说,了解SVM 和核函数的基本概念原理,知道模型是怎么运作的,在遇到问题的时候能够定位问题,并根据模型、方法的特性进行恰当的调整已经基本够用了。其他的再漫漫求索吧。
ps: hexo渲染公式有时出个bug真能逼死强迫症。

