上一篇对线性支持向量机的原理做了推导,这个推导的前提跟感知机模型一样,假设训练样本是线性可分的,也就是存在一个超平面能够将正负样本完全分隔开,但是这种假设在实际项目中存在的可能性跟国足挺进世界杯的可能性是一样一样的。
软间隔
上一篇文章中提到的间隔,严格来说应该称之为“硬间隔”,因为该间隔存在的前提是所有训练样本都要满足约束条件$y_i(w^Tx_i+b) \geq 1$,但是对于下图中的两类样本点,线性支持向量机并不适用,因为没办法在不映射到高维的情况下找到一条直线能把两个类别分隔开。

如果使用感知机的话,模型会无法收敛,并且找到的超平面有可能效果还可以也有可能很差。上图两个类别之间,混淆的样本点其实不多,总不能因为几颗芝麻就丢了西瓜吧。那么有没有办法使得支持向量机“容忍”这些不多的样本点出错,而保证绝大部分的样本点被正确分类呢,其中一个办法就是使用“软间隔”,允许某些样本不满足约束条件$y_i(w^Tx_i+b) \geq 1$,也就是让某些样本点满足条件$y_i(w^Tx_i+b) < 1$

软间隔最大化
为了获得最佳的划分超平面,还需要找出对应的损失函数来衡量划分超平面的效果。一方面,对于支持向量及以外的点,可以继续使用上一篇介绍的间隔最大化$\frac{2}{||w||}$来评估,也就是$min \frac{1}{2}||w||^2$;另一方面,对于支持向量内的点,没办法满足间隔大于等于1的约束条件,这种情况下,可以考虑引入松弛变量$\xi _i$ (其中$ \xi _i \geq 0$),使得函数间隔在加上松弛变量之后大于等于1,也就是:$$y_i(w^Tx_i+b) + \xi _i \geq 1 $$
将$\xi _i$挪到右边:$$y_i(w^Tx_i+b) \geq 1 -\xi _i $$
松弛变量可以理解为一种作用力,将误分类的点往正确分类的方向拉,拉回到对应的支持向量上。误分类的点与正确分类的边界越远,需要拉扯的力量越大,也就是$\xi_i$越大,对于支持向量后方的点,$\xi_i$值可以为0。
然后,同时对于误分类的点,给它一个惩罚因子(cost),用字母$C$表示($C \geq 0$),用来衡量误分类的代价,或者说,对离群点的重视程度(其尝试找出,在出现误分类的情况下,边界间隔最大的超平面以及保证数据点偏差量最小),这样损失函数就变成了:

这里的损失函数相对上篇只是多了后半部分。显然,对于惩罚因子$C$,当$C$无穷大时,表明只要有一个样本点是特异点的话就需要付出无限的代价,上面式子趋向于无穷大,这时将会使得所有的样本点都满足式子$y_i(w^Tx_i+b) \geq 1 $,这样的话软间隔最大化问题就变成硬间隔最大化问题(或者说是线性支持向量问题),但是由于给定的数据不是线性可分的,这样就会导致问题没有解;当$C$取有限值时,上式允许存在一些的样本不满足约束。
加上约束条件,目标函数变成如下凸二次规划问题:

跟支持向量机(一)中,目标函数的求解方式一样,可以通过拉格朗日乘子法得到对应的拉格朗日函数:

其中$\alpha _i \geq 0 , \mu _i \geq 0$是拉格朗日乘子。
一样的套路,求偏导,令$L(w,b,\alpha _i,\xi _i,\mu _i)$对$w,b,\xi _i$的偏导为0,可得:

将上面三个等式代入拉格朗日函数可以得到(公式推理写的有点宽,就不在这里展示了):
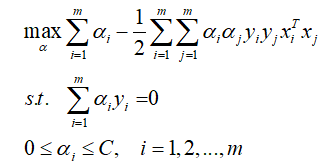
与上一篇相似,上式同样需要满足KKT条件,也就是要求:
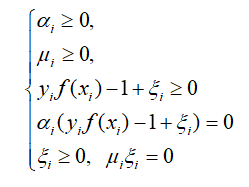
这里的$f(x_i)$其实就是$w^Tx_i+b$,通过KKT条件,我们能更加深入地了解SVM的本质–不管是硬间隔支持向量机还是软间隔支持向量机,最终根据模型求得的分隔超平面仅与支持向量有关。
对于上面KKT条件中的等式$\alpha_i(y_i f(x_i)-1+\xi _i)=0$,对于任意的训练样本,总会有$\alpha_i = 0$或者$y_i f(x_i)-1+\xi _i=0$,不妨把训练样本分为两种:支持向量以及支持向量以外的点,现在来分情况讨论下:
- $\alpha_i=0$,这个时候$y_i f(x_i)-1+\xi _i$等于任意值都是ok的,也就是$\alpha_i=0$的时候,不会对样本有任何的影响。如上一篇提到的那样,在衡量目标损失的时候,对于非支持向量(也就是支持向量以外的点),为了满足损失函数最大化,$\alpha_i$必定等于0。
- $\alpha_i> 0$,为了满足KKT条件,必然有$y_i f(x_i)-1+\xi _i=0$,也就意味着,样本$(x_i,y_i)$是支持向量
再结合偏导的等式$C=\alpha_i + \mu_i$ 和KKT条件$\mu_i \xi_i=0$、$\mu_i \geq 0$。由于$\mu_i$是大于等于0的,所以$\alpha_i$只能小于或等于$C$:

